Merge Sort is supposedly a good introduction to divide and conquer algorithms, greatly improving upon selection, insertion and bubble sort techniques, especially when input size increases.
Pseudocode:
— Recursively sort the first half of the input array. — Recursively sort the second half of the input array. — Merge two sorted sub-lists into one list.
C = output [length = n] A = 1st sorted array [n/2] B = 2nd sorted array [n/2] i = 0 or 1 (depending on the programming language) j = 0 or 1 (depending on the programming language)
for k = 1 to n
if A(i) < B(j) C(k) = A(i) i = i + 1
else if A(i) > B(j) C(k) = B(j) j = j + 1
Note: the pseudocode for the merge operation ignores the end cases.
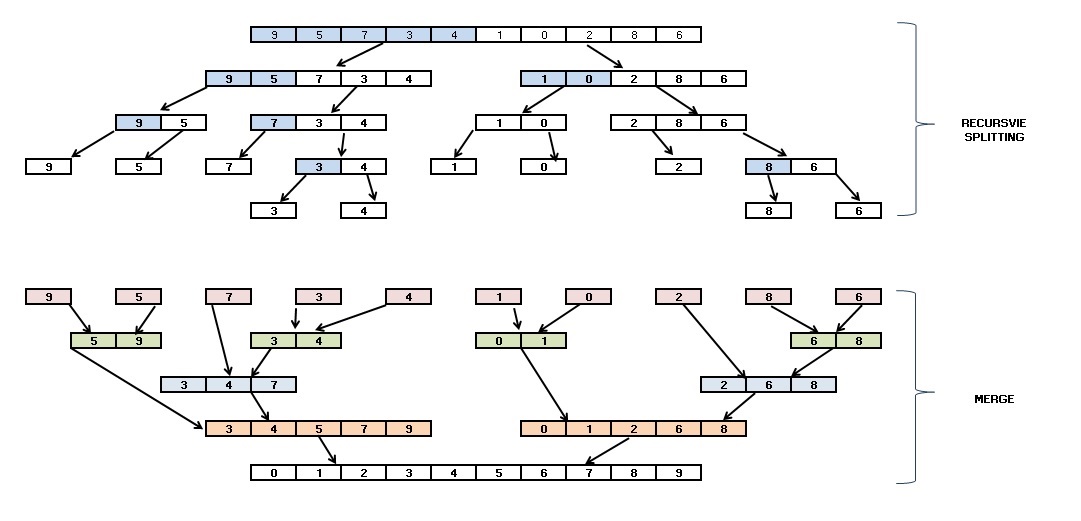
Visualizing the algorithm can be done in 2 stages — first, the recursive splitting of the arrays, 2 each 2 at a time, and second, the merge operation.
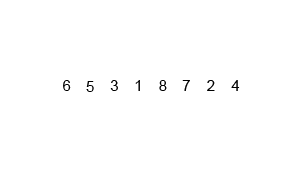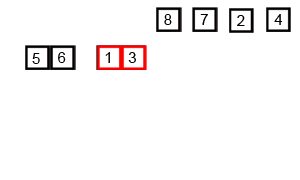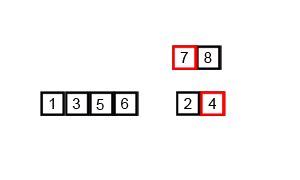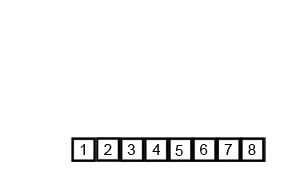
# Code for the merge subroutine
def merge(a,b):
""" Function to merge two arrays """
c = []
while len(a) != 0 and len(b) != 0:
if a[0] < b[0]:
c.append(a[0])
a.remove(a[0])
else:
c.append(b[0])
b.remove(b[0])
if len(a) == 0:
c += b
else:
c += a
return c
# Code for merge sort
def mergesort(x):
""" Function to sort an array using merge sort algorithm """
if len(x) == 0 or len(x) == 1:
return x
else:
middle = int(len(x)/2)
a = mergesort(x[:middle])
b = mergesort(x[middle:])
return merge(a,b)
x = [5,8,7,9,0,7]
x = mergesort(x)
print(x)
#Output: [5,8,7,9,0,7]
We can divide a list in half log2 n times where n is the length of the list. The second process is the merge. Each item in the list will eventually be processed and placed on the sorted list. So the merge operation which results in a list of size n requires n operations. The result of this analysis is that log2 n splits, each of which costs n for a total of nlog2 n operations.


